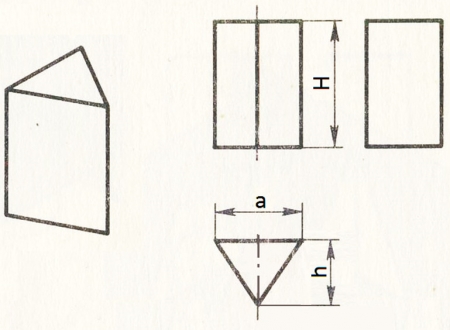
Regulāras trīsstūra prizmas projekcijas

4. attēlā parādīts, kā konstruēt regulāras trīsstūra prizmas aksonometriskās projekcijas (uzskatāmos attēlus). Lai aksonometriskajās projekcijās uzkonstruētu prizmas pamatu, no sākumpunkta O uz abām pusēm uzvelk x asi. Uz x ass pa labi un pa kreisi no O atliek pusi no trīsstūra malas (a/2). Uz y ass atliek trīsstūra augstumu h ortogonālajā izometrijā vai h/2 frontālajā dimetrijā. Iegūtos punktus savieno. No visām trijām virsotnēm paralēli z asij atliek prizmas augstumu H. Iegūtos punktus savieno.

4

 

5. attēlā redzams regulāras trīsstūra prizmas uzskatāmais attēls ortogonālajā izometrijā un trīs skati.

5

 

 

 

 

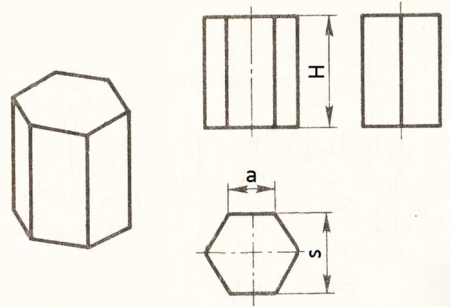
Regulāras sešstūra prizmas projekcijas

Pirms regulāra sešstūra konstruēšanas vēlams 6. attēlā izpētīt malu attiecības. Attālumu starp sešstūra pretējām malām, kas aptuveni vienāds ar ~1,75a, turpmāk apzīmēsim ar s.

6

7. attēlā parādīts, kā konstruēt regulāras sešstūra prizmas aksonometriskās projekcijas (uzskatāmos attēlus). Lai aksonometriskajās projekcijās uzkonstruētu prizmas pamatu, no sākumpunkta O uz abām pusēm uzvelk x un y asis, jo punkts O būs sešstūra viduspunkts. Uz x ass pa labi un pa kreisi no O atliek sešstūra malas garumu a. Uz y ass no O uz abām pusēm atliek attālumu s/2 ortogonālajā izometrijā vai s/4 frontālajā dimetrijā. Caur punktiem, kas iegūti uz y ass, velk paralēlas taisnes x asij. Uz tām pa labi un kreisi no y ass atliek pusi no sešstūra malas (a/2). Iegūtos punktus savieno. No visām sešām virsotnēm paralēli z asij atliek prizmas augstumu H. Iegūtos punktus savieno.

7

 

8. attēlā redzams regulāras sešstūra prizmas uzskatāmais attēls ortogonālajā izometrijā un trīs skati.

8