|
Taisnes pāreja riņķa līnijā
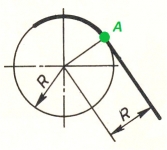
Taisnes pāreja riņķa līnijā būs laidena tikai tad, ja taisne pieskarsies riņķa līnijai. Tādā gadījumā salaiduma punkts A atradīsies uz rādiusa, kas perpendikulārs dotajai taisnei.
Taisnes un riņķa līnijas salaidums (ārējais)
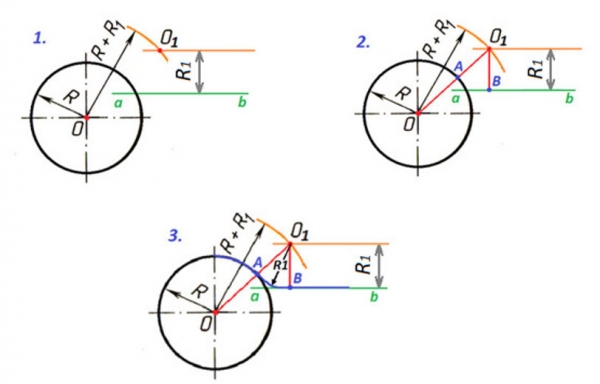
Dota riņķa līnija ar rādiusu R, taisnes nogrieznis ab un salaiduma loka rādiuss R1. 1. Lai atrastu salaiduma centru, riņķa līnijas centrā O liek cirkuļa kājiņu un novelk palīgloku ar rādiusu R+R1. Attālumā R1 no taisnes ab novelk tai paralēlu taisni līdz krustpunktam ar palīgloku. Iegūtais krustpunkts O1 ir salaiduma centrs. 2. Savienojot punktus O un O1, uz riņķa līnijas iegūst salaiduma punktu A. Novelkot no punkta O1 perpendikulu pret taisni ab, atrod otru salaiduma punktu B. 3. Savienojot ar loku (rādiuss R1) salaiduma punktus A un B, izveidojas riņķa līnijas un taisnes laidena pāreja.
Taisnes un riņķa līnijas salaidums (iekšējais)
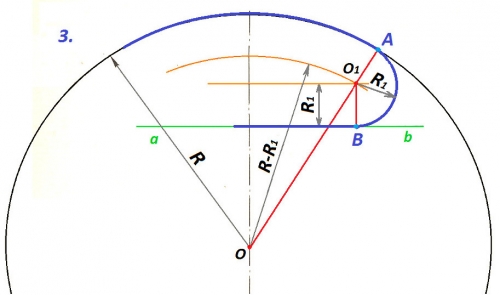
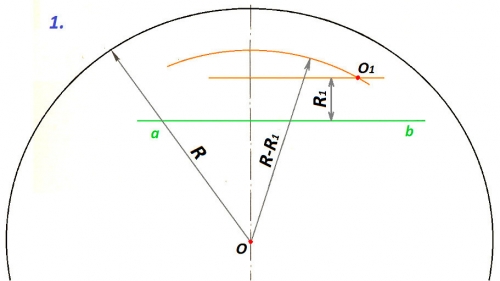
Dota riņķa līnija ar rādiusu R, taisnes nogrieznis ab un salaiduma loka rādiuss R1. 1. Lai atrastu salaiduma centru, riņķa līnijas centrā O liek cirkuļa kājiņu un novelk palīgloku ar rādiusu R-R1. Attālumā R1 no taisnes ab novelk tai paralēlu taisni līdz krustpunktam ar palīgloku. Iegūtais krustpunkts O1 ir salaiduma centrs.
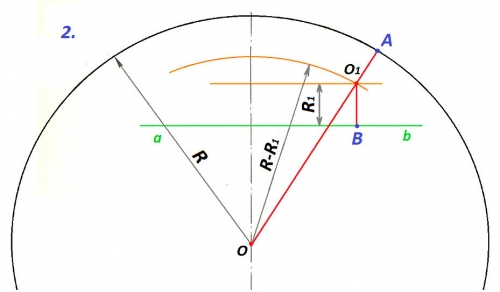
2. Savienojot punktus O un O1, uz riņķa līnijas iegūst salaiduma punktu A. Novelkot no punkta O1 perpendikulu pret taisni ab, atrod otru salaiduma punktu B.
3. Savienojot ar loku (rādiuss R1) salaiduma punktus A un B, izveidojas riņķa līnijas un taisnes laidena pāreja.
|
Mājas lapā ievietoti oriģināli autores darbi, nevis kopijas vai tulkojumi no citām tīmekļa vietnēm. Rakstus, zīmējumus, idejas un fotogrāfijas nedrīkst pārpublicēt bez autores piekrišanas, kā arī nedrīkst izmantot komerciāliem mērķiem.
© Sanita Nikitenko |
| Aizkulises
Kā uzskates materiāli izmantoti pārveidoti grāmatu attēli.
Sergejs Bogoļubovs “Rasēšana” (1990)
Viktors Vinogradovs un Igors Višņepoļskis “Rasēšana 1. daļa” (1988) |