|
Ja detaļas attēlo dabiskā lielumā, tad iegūst pareizu priekšstatu par to patiesajiem izmēriem. Šāda attēlošana bieži vien nav iespējama detaļas izmēru dēļ. Tādā gadījumā rasējumus izpilda samazinātā vai palielinātā veidā, tas ir, kādā noteiktā mērogā. Mērogs ir rasējuma izmēru attiecība pret detaļas izmēriem dabā. Rasējumos tiek izmantoti standartos noteikti mērogi (1).
|
|||||
|
1. lappusē - Riņķa līnijas dalīšana 3, 6 un 12 vienādās daļās. 2. lappusē - Riņķa līnijas dalīšana 4 un 8 vienādās daļās. 3. lappusē - Riņķa līnijas dalīšana 7, 5 un 10 vienādās daļās.
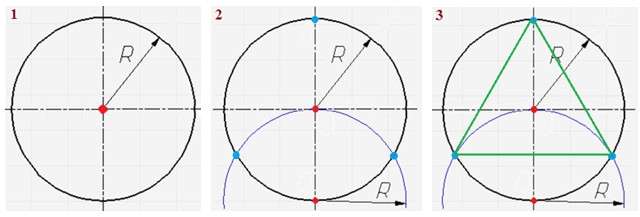
Daudzi mehānismi sastāv no detaļām, kuru elementi vienmērīgi izkārtojas pa riņķa līniju. Lai izgatavotu šādas detaļas rasējumu, jāprot riņķa līniju sadalīt noteikta skaita vienādās daļās. Atkarībā no daļu skaita, riņķa līniju var sadalīt ar transportieri, trīsstūriem vai cirkuli. Šajā tēmā doti piemēri, kā riņķa līniju sadalīt vienādās daļās ar cirkuli. Katrā lappusē parādīti riņķa līnijas dalīšanas paņēmieni, kas savā starpā līdzīgi. Ja nepieciešams riņķa līniju sadalīt daļās, kas piemēros nav dotas, jālieto speciāla koeficientu tabula, pēc kuras aprēķina hordas garumu, kas dala riņķa līniju. Šī horda ir arī regulāra daudzstūra, kas veidojas riņķa līnijas iekšpusē, malas garums.
Zīmējot riņķa līniju jāatceras, ka tai jāparāda simetrijas asis. To attēlošanai izmanto šauru svītrpunktu līniju. Pie tam centra vieta jānorāda ar svītru krustpunktu nevis ar punktu (1). Ja riņķa līnijas diametrs mazāks par 12 mm, tad simetrijas asis attēlo ar šauru nepārtrauktu līniju (2). Simetrijas asu galiem jāpārsniedz riņķa līnijas kontūra 3…5 mm garumā (3).
Riņķa līnijas dalīšana 3 vienādās daļās
|
|||||
|
1. lappusē - Divu taišņu salaidums. 2. lappusē - Taisnes un riņķa līnijas salaidums. 3. lappusē - Divu riņķa līniju saskare un salaidums.
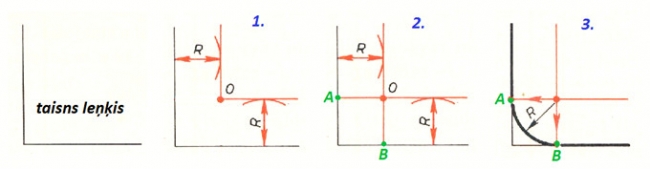
Mehānismos ir tādas detaļas, kuru kontūras veido taisnes un riņķu loki, kas laideni pāriet cits citā. Lai konstruētu šādas pārejas, rasējumos lieto salaidumus. Izšķir divu taišņu salaidumus; taisnes un riņķa līnijas salaidumus un divu riņķa līniju salaidumus.
Divu taišņu salaidums
Dotas divas taisnes, leņķis starp tām un salaiduma loka rādiuss R. 1. Paralēli abām taisnēm attālumā R no tām novelk taisnes, kuru krustpunkts ir salaiduma centrs O. 2. No salaiduma centra O velk perpendikulus pret abām taisnēm, iegūstot salaiduma punktus A un B. 3. Novieto cirkuļa kājiņu salaiduma centrā O un starp salaiduma punktiem A un B novelk loku ar rādiusu R.
|
|||||
|
1. lappusē - Ovāli. 2. lappusē - Ovoīdi. 3. lappusē - Spirāllīknes.
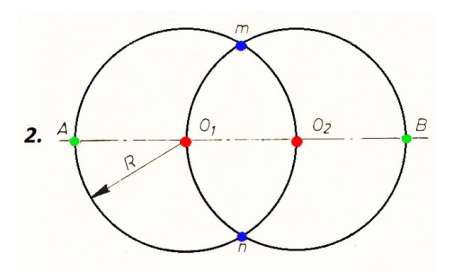
Cirkuļlīknes ir līknes, kuras veido riņķa līniju loki ar dažādiem rādiusiem. Pie cirkuļlīknēm pieder ovāli, ovoīdi un spirāllīknes.
Ovāls
1. veids. Dota ovāla garākā ass AB. 1. Asi AB sadala 3 vienādās daļās (AO1; O1O2; O2B). 2. Ar rādiusu R, kas vienāds ar attālumu O1O2, caur centriem O1 un O2 velk riņķa līnijas, kuras krustojas punktos m un n. |
|||||
Mājas lapā ievietoti oriģināli autores darbi, nevis kopijas vai tulkojumi no citām tīmekļa vietnēm. Rakstus, zīmējumus, idejas un fotogrāfijas nedrīkst pārpublicēt bez autores piekrišanas, kā arī nedrīkst izmantot komerciāliem mērķiem.
© Sanita Nikitenko |
||
Tumši pelēkās krāsas datumos ievietoti raksti. |
||
aksesuāri apģērbi atstarotāji audiopasakas ceļojumi dārzam DATOREKRĀNAM datorgrafika dizains un tehnoloģijas filcēšana filmas FOTOGRĀFIJAS GRĀMATAS IZLAIDUMAM izrādes un koncerti JĀŅIEM joki jubilejai koka lietas Lieldienām ludziņas MĀJOKLIM papīrdarbi pīšana un siešana ROTAĻAS un PARADUMI rotaļlietas sacensības skolai SPĒLES stāstiņi ŠŪŠANA AR ROKĀM šūšana ar šujmašīnu tamborēšana TEHNISKĀ GRAFIKA tekstilkrāsas VIZUĀLĀ MĀKSLA Ziemassvētkiem |
||
Ja mūsu domas materializējas, varbūt mirušie tās spēj lasīt. Tad arī mana dienasgrāmata kļūst par tiltu starp esamību un neesamību, starp dzīvajiem un mirušajiem. |
||
|
||
|